Question

Using the method of completing the square, put each circle into the form


`(x-h)^(2) + (y-k)^(2) = r^(2)`
Then determine the center and radius of each circle


`4x^(2) -4x + 4y^(2) - 59 = 0`

Answer 1

Standard form:
`(x-(1)/(2))^2 + (y-0)^2 = 15`

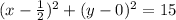
Center:
`((1)/(2), 0)`

Radius:
`r =√(15)`

Explanation:

The equation of a circle in the standard form is

`(x-h)^(2) + (y-k)^(2) = r^(2)`

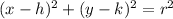
Where the point (h, k) is the center of the circle

To transform this equation
`4x^(2) -4x + 4y^(2) - 59 = 0` this equation in the standard form we use the method of square.

First, we group similar variables

`(4x^(2) -4x) + (4y^(2)) - 59 = 0`

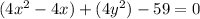
Divide both sides of equality by 4

`(x^(2) -x) + (y^(2)) - 14.75 = 0`

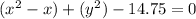
Now we complete square for variable x.

Take the coefficient "b" that accompanies the variable x and divide by 2. Then, elevate the result to the square:

`b =-1\\\\(b)/(2)= (-1)/(2)= -(1)/(2)\\\\((b)/(2))^2=  (-(1)/(2))^2 = (1)/(4)`

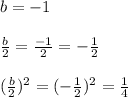
Now add
`((b)/(2))^2` on both sides of the equality

`(x^(2) -x +(1)/(4)) + (y^(2)) - 14.75 = ((1)/(4))`

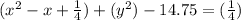
Factor the expression and simplify the independent terms

`(x-(1)/(2))^2 + (y^(2)) = 15`

`(x-(1)/(2))^2 + (y-0)^2 = 15`

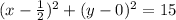
Then

`h =(1)/(2)\\\\k=0`

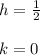
and the center is
`((1)/(2), 0)`

radius
`r =√(15)`