Question

Which pair of functions is not a pair of inverse fuctions

Answer 1

D is the answer,that is the incorrect inverse function.

Explanation:

For the first one

g(x)=6x-1

Let y=6x-1

6x=y+1

x=y+1/6

Therefore the inverse equation will be

x+1/6 so,the first equation is right.

The second one

g(x)=19x+4

Let y=19x+4

19x=y-4

x=y-4/19 so,the second function is right.

For the last one

f(x)=x/x+20

y=x/x+20

y(x+20)=x

x+20=x/y

x=x/y-20

g(x)=x/y-20,so the function is wrong and that is the aswer.

Answer 2

The pair of functions that is not inverse functions are:

`f(x)=(x)/(x+20)\ and\ g(x)=(20x)/(x-1)`

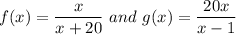
Explanation:

We know that two functions a and b are said to be inverse of each other if:

f(g(x))=g(f(x))=x

i.e. the compositions of the function gives identity.

and the inverse of the given function is calculated by equation the function to y and then calculating the value of x in terms of y.

and the function in terms of y is the inverse function.

A)

`f(x)=(x+1)/(6)`

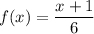
Now if f(x)=y then

`(x+1)/(6)=y\\\\\\x+1=6y\\\\\\x=6y-1\\\\\\g(x)=6x-1`

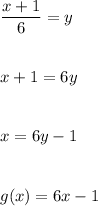
B)

`f(x)=(x-4)/(19)\\\\\\f(x)=y\\\\\\(x-4)/(19)=y\\\\\\x=19y+4`

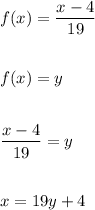
i.e.

`g(x)=19x+4`

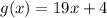
C)

`f(x)=x^5\\\\\\f(x)=y\\\\\\x^5=y\\\\\\x=\sqrt[5]{y}`

i.e. we have:

`g(x)=\sqrt[5]{x}`

D)

`f(x)=(x)/(x+20)`

if f(x)=y then

`(x)/(x+20)=y\\\\\\x=xy+20y\\\\\\x(1-y)=20y\\\\x=(20y)/(1-y)`

`g(x)=(20x)/(1-x)\\eq (20x)/(x-1)`

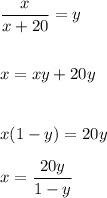
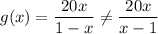
Hence, option: D is the answer.