Answer:

Explanation:
Given:It is given that Chords AB and CD intersect each other at point E.
To find: The measure of ∠BEC.
Construction: Join AC.
Solution:
It is given that Chords AB and CD intersect each other at point E.
Now, we know that the inscribed angle is the half of the intercepted arc, thus
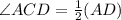
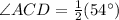
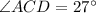
And,
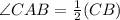
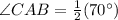
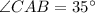
Now, in ΔAEC, we have
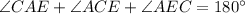 (Angle sum property of triangles)
(Angle sum property of triangles)
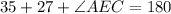
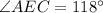
Also, using the straight line property, we have
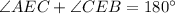

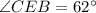
Therefore, the measure of
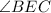 is
is
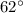 .
.