Question

What is the height of the given pyramid if the volume is 48 cubic units? Question 3 options: 4 6 7 5

Answer 1

`\bf \textit{volume of a pyramid}\\\\ V=\cfrac{1}{3}Bh~~ \begin{cases} B=area~of\\ \qquad its~base\\ h=height\\[-0.5em] \hrulefill\\ B=\stackrel{6* 6}{36}\\ V=48 \end{cases}\implies 48=\cfrac{1}{3}(36)h\implies 48=12h \\\\\\ \cfrac{48}{12}=h\implies 4=h`

Answer 2

Height of the pyramid is:

4 units

Explanation:

Here we are given a right rectangular pyramid

Whose Volume is given by:

`V=(lwh)/(3)`

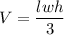
where l and w is the length and width of its base and h is the height of the pyramid

Here, we are given l=b=6 units

We have to find h

`V=(6* 6* h)/(3)\\ \\48=6* 2* h\\\\48=12* h\\\\h=4`

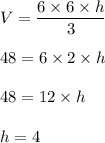
Hence, height of the pyramid is:

4 units