Question

Components of a vector

Answer 1

QUESTION 13.

The given vector has the initial point at
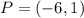`P=(-6,1)`; and terminal point at
`Q=(4,-4)`

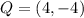
We want to write vector
`v` in the form:
`ai+bj`.

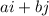Using position vectors, we have;

`v=^(\rightarrow)_(OQ)-^(\rightarrow)_(OP)`

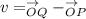
This implies that;

`v=\binom{4}{-4}-\binom{-6}{1}`

`v=\binom{4--6}{-4-1}`

`v=\binom{10}{-5}`

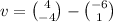
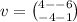
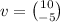
We now write this in the required form;

`v=10i-5j`

QUESTION 14

It was given that;

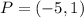`P=(-5,1)` and Q=(x,-14).

`^(\to)_(PQ)=^(\to)_(OQ)-^(\to)_(OP)`

`^(\to)_(PQ)=\binom{x}{-14}-\binom{-5}{1}`

`^(\to)_(PQ)=\binom{x--5}{-14-1}`

`^(\to)_(PQ)=\binom{x+5}{-15}`

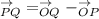
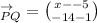
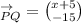
If the length of this vector is 25, then we can solve the following equation for x.

`√((x+5)^2+(-15)^2) =25`

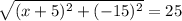
We square both sides to get;

`(x+5)^2+(-15)^2=25^2`

`(x+5)^2+225=625`

`(x+5)^2=625-225`

`(x+5)^2=400`

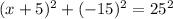
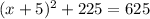
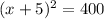
Take the square root of both sides to get;

`x+5=\pm √(400)`

`x+5=\pm20`

`x=-5\pm20`

`x=-25,x=15`

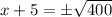
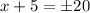
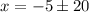
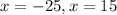
QUESTION 15

The given vector, has magnitude
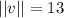`||v||=13` and makes an angle of
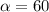`\alpha=60\degree` with the positive x-axis.

The components of this vector is given by

`v=\binomv \sin \alpha`

`v=\binom{13 \cos 60\degree}{13\sin 60\degree}`

`v=\binom{(13)/(2)}{(13√(3))/(2)}`

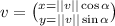
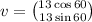
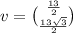
Hence the required form is;

`v=(13)/(2)i+(13√(3))/(2)j`

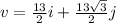
QUESTION 16.

The given vector, has magnitude
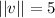`||v||=5` and makes an angle of
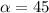`\alpha=45\degree` with the positive x-axis.

The components of this vector is given by

`v=\binomy=`

`v=\binom{5 \cos 45\degree}{5\sin 45\degree}`

`v=\binom{(5√(2))/(2)}{(13√(3))/(2)}`

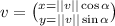
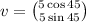
Hence the required form is;

`v=(5√(2))/(2)i+(5√(2))/(2)j`

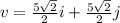
QUESTION 17

The given vector, has magnitude
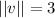`||v||=3` and makes an angle of
`\alpha=270\degree` with the positive x-axis.

The components of this vector is given by

`v=\binomvv`

`v=\binom{3 \cos 270\degree}{13\sin 270\degree}`

`v=\binom{0}{-1}`

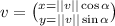
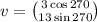
Hence the required form is;

`v=0i-j`

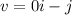
QUESTION 18

The given vector is;

`v=-i+√(3)j`

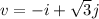
This vector is in the second quadrant, because the x-component is negative and the y-component is positive.

The direction angle is given by;

`\tan(\alpha)=(y)/(x)`

`\tan(\alpha)=(√(3) )/(-1)=-√(3)`

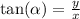
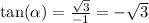
This implies that;

`\alpha=120\degree`

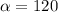
The direction angle of the vector is 120 degrees.

QUESTION 19

The given vector is;

`v=-i+3j`

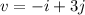
This vector is in the second quadrant, because the x-component is negative and the y-component is positive.

The direction angle is given by;

`\tan(\apha)=(y)/(x)`

`\tan(\alpha)=(3)/(-1)=-3`

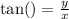
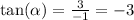
This implies that;

`\alpha=108.4\degree`

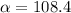
The direction angle of the vector is 1O8.4 degrees to one decimal place.

QUESTION 20

We want to find the angle between the vectors,

`v=8i+6j`

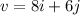
and

`w=4i+9j`

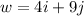
The angle between the two vectors is given by;

`\cos \theta=(v\bullet w)/(||v||\:||w||)`

`\cos \theta=((8i+6j)\bullet (4i+9j))/((√(8^2+6^2) )(√(4^2+9^2)))`

`\cos \theta=((8*4+6*9))/((√(64+36) )(√(16+81)))`

`\cos \theta=(32+54)/((√(64+36) )(16+81))`

`\cos \theta=(86)/((√(100) )(√(97)))`

`\cos \theta=0.8732`

`\theta=\cos^(-1)(0.8732)`

`\theta=29.2\degree`

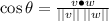
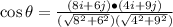
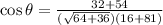
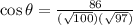
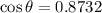
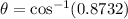
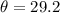
The angle between the two vectors is 29.2 degrees to one decimal place.