Answer:
A.
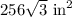
Explanation:
Please find the attachment.
We have been given an image of a square pyramid ABCDE. We are asked to find the lateral area of pyramid.
First of all we need to find the height of pyramid.
The lateral height of the pyramid will be the length of altitude drawn from the lateral face of pyramid to the base of pyramid.
Since the base of pyramid is square, so the length of segment CM will be half the length of BC that is 16.
Since tangent relates the opposite and adjacent sides of a right triangle, so we can find the lateral height as:
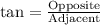
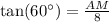

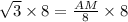
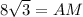
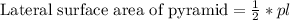 , where,
, where,
p = Perimeter of the base,
l = Lateral or slant height.
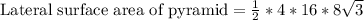
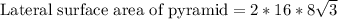

Therefore, the lateral surface area of our given pyramid is
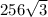 square inches and option A is the correct choice.
square inches and option A is the correct choice.