Question

A small airplane can hold 44 passengers.fifteen passengers board the plane a. Identify an inequality that represents the additional number of passengers,p, that can board the plane. •15+p<= 44•p—44<=15 • 15+p>=44•15+p<=44. Solve the inequality, the solution is: B. Which best explains whether or not 30 more passengers can board the plane. Please solve this

Answer 1

Answers:

Inequality is
`15 + p \le 44`

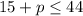
Choice A) 30 more passengers cannot board the plane. Only 29 more passengers can board the plane

===============================================

Step-by-step explanation:

15 people are already on the plane.

p is a placeholder for a positive whole number representing the additional number of people that can get on the plane.

In total, the plane holds 15+p individuals.

This expression's largest possible value is 44. Think of it as the ceiling. In terms of math, we call it the maximum. Since at most 44 people can be on the plane, this means the inequality we'll set up is
`15+p \le 44`

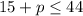
This says "15+p is less than or equal to 44". It's the same as saying "15+p is 44 or smaller".

---------------------------

To isolate p, we subtract 15 from both sides

Doing so leads to...

`15+p \le 44\\\\15+p-15 \le 44-15\\\\p \le 29`

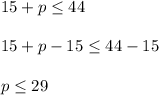
We can see that the largest p can get is 29, meaning that at most 29 more people can board the plane. There's no way that 30 people can board. That unfortunate 30-29 = 1 person must wait for another plane.

This all shows why choice A is the answer.

----------------------------

As a way to check the answer, we can note how p = 29 leads to 15+p = 15+29 = 44. We've filled the plane to full capacity.

If p = 30, then 15+p = 15+30 = 45, and we've gone 1 seat overboard.