Question

Q4
Help pleaseeeeeeee

Answer 1

a. The general equation for a circle centered at
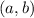`(a,b)` with radius
`r` is

`(x-a)^2+(y-b)^2=r^2`

The described circle has equation

`(x+3)^2+(y+2)^2=r^2`

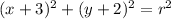
We know the circle passes through the origin. This means that the equation above holds for
`x=0` and
`y=0`. The distance between any point on the circle and its center is the radius, so we can use this fact to determine
`r`:

`(0+3)^2+(0+2)^2=r^2\implies 9+4=13=r^2\implies r=√(13)`

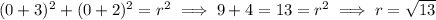
So the circle's equation is

`(x+3)^2+(y+2)^2=(√(13))^2=13`

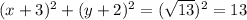
b. If the distance between point B and the center is less than
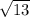`√(13)`, then B lies inside the circle. If the distance is greater than
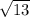`√(13)`, it falls outside the circle. Otherwise, if the distance is exactly
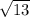`√(13)`, then B lies on the circle.

The distance from B to the center is

`√((-1+3)^2+(3+2)^2)=√(4+25)=√(29)`

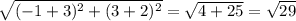
`29>13`, so
`√(29)>√(13)`, which means B falls outside the circle.