Question

An object is 16.0cm to the left of a lens. The lens forms an image 36.0cm to the right of the lens.

Part A What is the focal length of the lens?
Part B Is the lens converging or diverging?
Part C If the object is 8.00 mm tall, how tall is the image?
Part D Is it erect or inverted?

Answer 1

A) 11.1 cm

We can find the focal length of the lens by using the lens equation:

`(1)/(f)=(1)/(p)+(1)/(q)`

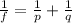
where

f is the focal length

p = 16.0 cm is the distance of the object from the lens

q = 36.0 cm is the distance of the image from the lens (taken with positive sign since it is on the opposide side to the image, so it is a real image)

Solving the equation for f:

`(1)/(f)=(1)/(16.0 cm)+(1)/(36.0 cm)=0.09 cm^(-1)\\f=(1)/(0.09 cm^(-1))=11.1 cm`

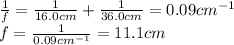
B) Converging

The focal length is:

- Positive for a converging lens

- Negative for a diverging lens

In this case, the focal length is positive, so it is a converging lens.

C) 18.0 mm

The magnification equation states that:

`(h_i)/(h_o)=-(q)/(p)`

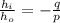
where

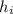`h_i` is the heigth of the image

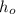`h_o` is the height of the object

`q=36.0 cm`

`p=16.0 cm`

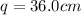
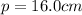
Solving the formula for
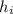`h_i`, we find

`h_i = -h_o (q)/(p)=-(8.00 mm)(36.0 cm)/(16.0 cm)=-18.0 mm`

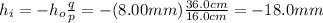
So the image is 18 mm high.

D) Inverted

From the magnification equation we have that:

- When the sign of
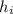`h_i` is positive, the image is erect

- When the sign of
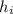`h_i` is negative, the image is inverted

In this case,
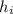`h_i` is negative, so the image is inverted.