Answer:
x=2 ; x=-4 or x=-3/2
Explanation:
We are given a cubic polynomial
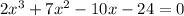
Here as we are having a cubic equation to factorize, we have to find some value of x such that when we put that value in place of x , it gives us a 0. We have to try it randomly like first we try it for x=1 then x=2 and so on.
On trying for x=2 , we see that the equation becomes 0=0 and hence x=2 is one of the solution. And also as x=2 is one of the solution, (x-2) must be one of the factor. Now we use this property to determine the other factor like this.
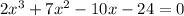
Adding and subtracing
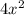 to
to
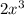 we get
we get
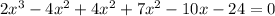
Now we take out
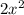 as GCF
as GCF

Now subtracting and adding
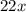 to
to
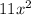
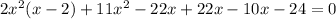
taking
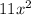 as GCF out
as GCF out
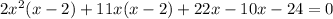

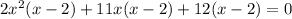
Now taking
 out as GCF
out as GCF
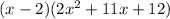
Now we need to split the middle term of
 to factorize it in such a way that their product is 2*12 and sum is 11. We have 8 and 3 as these factors.
to factorize it in such a way that their product is 2*12 and sum is 11. We have 8 and 3 as these factors.
Hence it can be factored like this
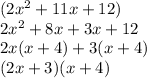
Hence our answer will be

And thus the solutions will be
x-2=0 : x=2
x+4=0 ; x=-4
2x+3=0 ; x=-
