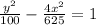Question

Find an equation in standard form for the hyperbola with vertices at (0, ±10) and asymptotes at y = ±five divided by four times x..

Answer 1

The equation of the hyperbola in standard form is

`(y^(2))/(100)-(4x^(2))/(625)=1`

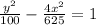
Explanation:

* We will take about the standard form equation of the hyperbola

- If the given coordinates of the vertices (0 , a) and (0 , -a)

∴ The transverse axis is the y-axis. (because x = 0)

- If the given asymptotes at y = ± (b/a) x

∴ Use the standard form ⇒ y²/a² - x²/b² = 1

* Lets use this to solve our problem

∵ The vertices are (0 , 10) and (0 , -10)

∴ a = ±10

∴ a² = 100

∵ The asymptotes at y = ± 5/4 x

∴ ± 5/4 = ± b/a

∵ a = ± 10

∴ ± 5/4 = ± b/10 ⇒ using cross multiplication

∴± (4b) = ± (5 × 10) = ± 50 ⇒ divide both sides by 4

∴ b = ± 25/2

∴ b² = 625/4

* Now Lets write the equation

* y²/100 - x²/(625/4) = 1

∵ x² ÷ 625/4 = x² × 4/625 = (4x²/625)

∴ y²/100 - 4x²/625 = 1

* The equation of the hyperbola in standard form is

`(y^(2))/(100)-(4x^(2))/(625)=1`