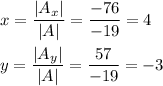Question

Identify the determinants for the given

Answer 1

Step-by-step explanation:

The first determinant is that of the matrix of coefficients:

`|A|=\left|\begin{array}{cc}5&2\\-3&-5\end{array}\right|=(5)(-5)-(-3)(2)=-19`

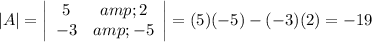
The second determinant is the same as the above but with the constants substituted for the x-coefficients.

`|A_x|=\left|\begin{array}{cc}14&2\\3&-5\end{array}\right|=(14)(-5)-(3)(2) =-76`

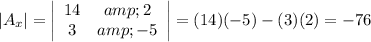
The third determinant is the same as the first but with the constants substituted for the y-coefficients.

`|A_y|=\left|\begin{array}{cc}5&14\\-3&3\end{array}\right|=(5)(3)-(-3)(14)=57`

_____

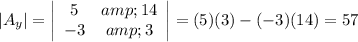
The solution to the system of equations is then ...

`x=(|A_x|)/(|A|)=(-76)/(-19) =4\\\\y=(|A_y|)/(|A|)=(57)/(-19) =-3`