Question

Two arcades charge an entrance fee and a fee per game. At Arcade A, the total cosi y (in dollars) of playing 2 games is represented

by the linear function y=0.75.2 + 2. The table shows the total cost for playing I games at Arcade B. Determine which arcade is
described by each phrase below.
Number of Games,
0
4
8
12
Total Cost (dollars), y
8
10
12
14
Arcade A
Arcade B

higher fee per game
higher entrance fee
higher total cost for 8 games

​

Answer 1

Part a) Higher fee per game Arcade A

Part b) Higher entrance fee Arcade B

Part c) Higher total cost for 8 games Arcade B

Explanation:

Let

x------> the number of games

Arcade A

we have that the linear equation is

`y=0.75x+2`

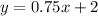
The fee per game is $0.75

The entrance fee is $2

The cost for 8 games is equal to

`y=0.75(8)+2=\$8`

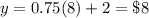
Arcade B

Find the linear equation

Let

`A(0,8),B(4,10)`

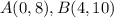
Find the slope of the line (fee per game)

`m=(10-8)/(4-0)=0.50`

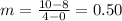
The point A is the y-intercept

The linear equation is

`y=0.50x+8`

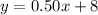
so

The fee per game is $0.50

The entrance fee is $8

The cost for 8 games is equal to

`y=0.50(8)+8=\$12`

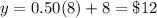
therefore

Part a) Higher fee per game Arcade A

Part b) Higher entrance fee Arcade B

Part c) Higher total cost for 8 games Arcade B