Answer:
The lateral area is
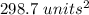
Explanation:
we know that
The lateral area of the regular octagonal pyramid is equal to the area of its eight triangular lateral faces
The lateral area is equal to
![LA=8[(1)/(2)(b)(l)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/whspwrqj8orfz4iq62zgzr7lh4ct95l9sd.png)
we have
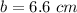
To find the slant height apply the Pythagoras Theorem
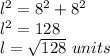
Find the lateral area
substitute the values
![LA=8[(1)/(2)(6.6)(√(128))]=298.7\ units^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/n5r8nrvbp18839lrkn0ph7zy4vtkvxrct4.png)