Answer:
71°
Explanation:
This is an isosceles triangle because it has two sides with lengths, hence the angles opposite the equal sides are also equal, that is ∠U = ∠V.
So we can say that:
∠U = ∠V = α
∠W = β
Since the internal angles of a triangle add up to 180 degrees, then:
α + α + β = 180
2α + β = 180
β = 180 - 2α
Using the law of sine:

Therefore:
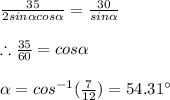
But we want to know ∠W = β, therefore:
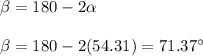
And rounded to the nearest degree:
∠W = 71°