Answer:
The surface area of the sphere is
![108\pi \sqrt[3]{3}\ in^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/icxc8f17zcb85fewoxhoqtbhx3176wzgj1.png)
Explanation:
In this problem the volume should be
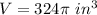 instead of
instead of
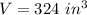
step 1
Find the radius of the sphere
The volume of the sphere is equal to
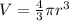
we have
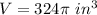
substitute and solve for r
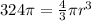
simplify
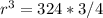
![r=\sqrt[3]{243}\ in](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1gz92fahw0goo5fj58dkv70yij8xm2j2xy.png)
step 2
Find the surface area of the sphere
The surface area of the sphere is equal to
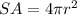
we have
![r=\sqrt[3]{243}\ in](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1gz92fahw0goo5fj58dkv70yij8xm2j2xy.png)
substitute
![SA=4\pi(\sqrt[3]{243})^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/l7owy5hpx8md2a26fk9d45lh7tf0zf895l.png)
simplify
Remember that
![(\sqrt[3]{243})^(2)=243^((2/3)) =27\sqrt[3]{3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/2f84chls0rxqpo0nschlkxrofek2k5qdjp.png)
![SA=4\pi(27\sqrt[3]{3})=108\pi \sqrt[3]{3}\ in^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/uwl1okc07lbx4xu7f7dhbz7yu3zx15k4yo.png)