Question

Find the point, M, that divides segment AB into a ratio of 2:3 if A is at (0, 15) and B is at (20, 0). A) (8, 9) B) (9, 9) C) (9, 12) Eliminate D) (8, 12)

Answer 1

A. (8,9)

Step-by-step explanation

The point that divides,

`A(x_1,y_1), B(x_2,y_2)`

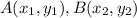
in the ratio m:n is given by

`x = (mx_2 + nx_1)/(m + n)`

`y= (my_2 + ny_1)/(m + n)`

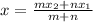
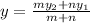
The given points are A(0,15) B(20,0)

the ratio is 2:3.

This implies that, m=2,n=3.

`x_1=0,x_2=20,y_1=15,y_2=0`

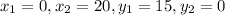
We plug in the values to get:

`x = (2 * 20 + 3 * 0)/(2+ 3)`

`x = (40)/(5) = 8`

`y= (2 * 0 + 3 * 15)/(2+ 3)`

`y= (45)/(5) = 9`

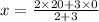
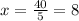
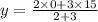
Hence the required point is

(8,9)

The correct answer is A.