Question

The vertices of a triangle are A(7,5) B(4,2) and C(9,2) what is mABC

Answer 1

A(7,5)

Explanation:

This is correct because the area of a triangle is b × h = a.

Answer 2

The measure of ∠ABC is 45°.

Explanation:

Given : The vertices of a triangle are A(7,5) B(4,2) and C(9,2).

To find : What is ∠ABC ?

Solution :

First we side the length of the sides,

Using Distance formula,

`d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

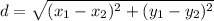
Length of side AB, A(7,5) and B(4,2)

`c= √((7-4)^2 + (5-2)^2) \\c= √((3)^2 + (3)^2) \\c= √(9+9) \\c= √(18)`

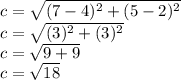
Length of side BC, B(4,2) and C(9,2)

`a= √((4-9)^2 +(2-2)^2) \\a= √((-5)^2 + 0) \\a= √(25) \\a= 5`

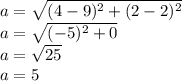
Length of the side AC, A(7,5) and C(9,2)

`b = √((7-9)^2 +(5-2)^2)\\ b= √((-2)^2 + (3)^2) \\b= √(4+ 9)\\b=√(13)`

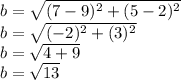
By the Law of Cosines,

`\cos B=(a^2 + c^2 -b^2)/(2ac)`

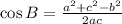
Substitute the values,

`\cos B=((5)^2 + (√(18))^2 - (√(13))^2)/(2* 5* √(18))`

`\cos B =(25+18-13)/(10√(18))`

`\cos B=(30)/(10√(18))`

`\cos B =(3)/(√(18))`

`\cos B= (3)/(3√(2))`

`\cos B= (1)/(√(2))`

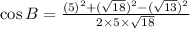
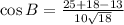
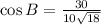
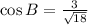
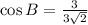
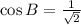
Taking Inverse Cosine function,

`B= \cos^(-1)( (1)/(√(2)))`

`B=45^\circ`

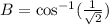
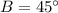
Therefore, The measure of ∠ABC is 45°.