Answer:
The number is +1
Explanation:
we have
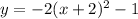
This is the equation of a vertical parabola with vertex at point (-2,-1)
The function has no real zeros
we know that
If the number +1 is added to the equation on the right side
then
 ------->
------->
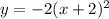
Is a translation one unit up
The vertex of the parabola will be the point (-2,0) and the function will have one real root
see the attached figure to better understand the problem