Answer:
The answer is ellipse; 30° ⇒ answer (d)
Explanation:
* At first lets talk about the general form of the conic equation
- Ax² + Bxy + Cy² + Dx + Ey + F = 0
∵ B² - 4AC < 0 , if a conic exists, it will be either a circle or an ellipse.
∵ B² - 4AC = 0 , if a conic exists, it will be a parabola.
∵ B² - 4AC > 0 , if a conic exists, it will be a hyperbola.
* Now we will study our equation:
* 13x² + 6√3xy + 7y² - 16 = 0
∵ A = 13 , B = 6√3 , C = 7
∴ B² - 4 AC = (6√3)² - 4(13)(7) = -256
∴ B² - 4AC < 0
∴ The graph is ellipse or circle
* If A and C are nonzero, have the same sign, and are not
equal to each other, then the graph is an ellipse.
* If A and C are equal and nonzero and have the same
sign, then the graph is a circle.
∵ A and C have same signs with different values
∴ It is an ellipse
* To find the angle of rotation use the rule:
- cot(2Ф) = (A - C)/B
∵ A = 13 , B = 6√3 , C = 7
∴ cot(2Ф) = (13 - 7)/6√3 = 6/6√3 = 1/√3
∵ tan(2Ф) = 1/cot(2Ф)
∴ tan(2Ф) = √3 ⇒ 2Ф =
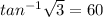
∴ 2Ф = 60°
∴ Ф = 30°
* The answer is ellipse; with angle of rotation = 30°