Answer:
Option c
Explanation:
The general polar form of the conic with cosine in the denominator is:
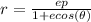
Comparing the given equation (Denominator) with the general equation, we can write:
e = 2
This means eccentricity = 2. Since eccentricity is greater than 1, the given conic is a hyperbola.
The equation of directrix is x = p
Comparing the numerators of general and given equation, we can write:
ep = 6
Using the value of e, we get p = 3
Therefore, equation of directrix is x =3
Hence option c is the correct answer.