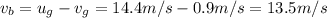a) 14.4 m/s
The problem can be solved by using the law of conservation of total momentum; in fact, the total initial momentum must be equal to the final total momentum:
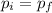
So we have:
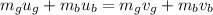 (1)
(1)
where
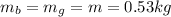 is the mass of each ball
is the mass of each ball
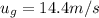 is the initial velocity of the green ball
is the initial velocity of the green ball
 is the initial velocity of the blue ball
is the initial velocity of the blue ball
 is the final velocity of the green ball
is the final velocity of the green ball
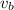 is the final velocity of the blue ball
is the final velocity of the blue ball
Simplifying the mass in the equation and solving for
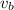 , we find
, we find
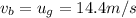
b) 12.0 m/s
This time, the green ball continues moving after the collision at
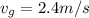
So the equation (1) becomes
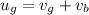
And solving for
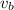 we find
we find
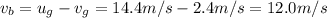
c) 13.5 m/s
This time, the green ball continues moving after the collision at
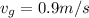
So the equation (1) becomes
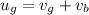
And solving for
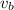 we find
we find