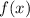Answer: OPTION C
Explanation:
Calculate the x-coordinate of the vertex of the parabola of the function
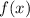 , with the following formula:
, with the following formula:
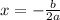
In this case:
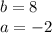
Substitute values:
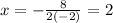
Substitute
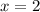 into the funtion
into the funtion
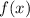 to find the y-coordinate of the vertex. Then:
to find the y-coordinate of the vertex. Then:
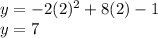
Therefore, the maximum value of
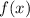 is:
is:
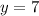
As you can see, the y-coordinate of the vertex of the parabola
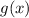 is less than 7, therefore, you can conclude that the function that has the greater maximum value is:
is less than 7, therefore, you can conclude that the function that has the greater maximum value is: