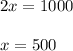Question

Solve the equation by using tu basic properties of logarithms log(2x)=3 (Picture provided)

Answer 1

Option b

Explanation:

According to the property of sum of logarithms we know that

`log(ab) = log(a) + log(b)`.

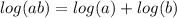In this case we have the equation:

`log(2x) = 3`

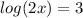
Using the property of sum of logarithms:

`log(2) + log(x) = 3`

`log(x) = 3 - log(2)`

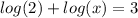
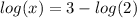
We also know that:

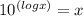`10 ^((logx)) = x` -------- Inverse logarithm

So:

`x = 10 ^(3-log(2))`

`x = 500`

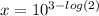
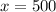
Another easiest way to solve it is the following:

Make
`w = 2x`.

Then:

`log(2x) = log(w)`

`log(w) = 3`

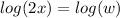
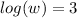
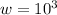`w = 10^3` -------- Inverse logarithm property

`w = 1000`

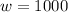
but
`w= 2x`. Then:

`2x = 1000\\\\x = 500`