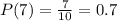Question

Find the probability distribution for the following function: P(x) = x/10 for x = 3, 5, and 7

Answer 1

`P(3)=(3)/(10)=0.3\\\\P(5)=(5)/(10)=0.5\\\\P(7)=(7)/(10)=0.7`

Explanation:

Probability is the possibility of happening of some event .

Probability =
`(No.\,\,of\,\,outcomes)/(Total\,\,no.\,\,of\,\,outcomes)`

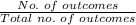
Probability distribution links each outcome of an experiment with it's probability of occurrence .

Given:
`P(x)=(x)/(10)`

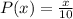
To find: Probability distribution for the given function for x = 3 , 5 and 7

Solution:

For x = 3 :

On putting x = 3 in function
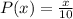`P(x)=(x)/(10)` , we get

`P(3)=(3)/(10)=0.3`

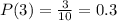
For x = 5 :

On putting x = 5 in function
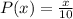`P(x)=(x)/(10)` , we get

`P(5)=(5)/(10)=0.5`

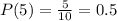
For x = 7 :

On putting x = 7 in function
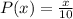`P(x)=(x)/(10)` , we get

`P(7)=(7)/(10)=0.7`

Answer 2

3/10. 1/2 and 7/10

Explanation:

For P(x) = x/10

When x = 3;

Then;

P(3) = 3/10

When x = 5

Then;

P(5) = 5/10

= 1/2

When, x = 7

Then;

P(7) = 7/10