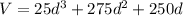Answer:
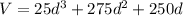
Explanation:
If the pool has a rectangular shape then its volume can be written as:
V = Width * Length * Depth
Let's call:
w = width
l = length
d = depth.
So we know from the statement of the problem that:

 (5 feet more than 5 times the depth)
(5 feet more than 5 times the depth)
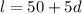 (50 feet more than 5 times the depth)
(50 feet more than 5 times the depth)
Then, the volume can be written according to the depth as:
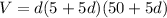
![V = d[250 + 25d + 250d + 25d ^ 2]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/xzr1drwmuq274fffofqnj3ytmuvmepx8uw.png)