Answer:
True
Explanation:
To answer this question we must evaluate
y = 0° on both sides of the equation.
For the left side we have:
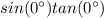
We know that
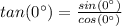
We know that
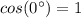 and
and
 .
.
Therefore
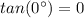 .
.
Then the left-hand side of the equals is equal to zero.
On the right side we have:
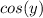
When evaluating
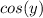 at
at
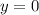
We have to
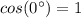 .
.
0 ≠ 1
The equation is not satisfied. Therefore y = 0 ° is a counterexample to the equation