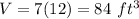Question

A water trough has two congruent isosceles trapezoids as ends and two congruent rectangles as sides. The exterior surface area of the trough is ________. The volume of the trough is _____. If a trough is emptied until the water level is even with the midsegment of the trapezoidal ends there will be ______ cubic feet of water left in the trough.

Answer 1

Part a) The exterior surface area is equal to
`160\ ft^(2)`

Part b) The volume is equal to
`240\ ft^(3)`

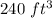
Part c) The volume water left in the trough will be
`84\ ft^(3)`

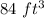
Explanation:

Part a) we know that

The exterior surface area is equal to the area of both trapezoids plus the area of both rectangles

so

Find the area of two rectangles

`A=2[12*5]=120\ ft^(2)`

Find the area of two trapezoids

`A=2[(1)/(2)(8+2)h]`

Applying Pythagoras theorem calculate the height h

`h^(2)=5^(2)-3^(2)\\h^(2)=16\\h=4\ ft`

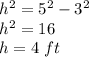
substitute the value of h to find the area

`A=2[(1)/(2)(8+2)(4)]=40\ ft^(2)`

The exterior surface area is equal to

`120\ ft^(2)+40\ ft^(2)=160\ ft^(2)`

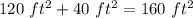
Part b) Find the volume

we know that

The volume is equal to

`V=BL`

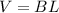
where

B is the area of the trapezoidal face

L is the length of the trough

we have

`B=20\ ft^(2)\\ L=12\ ft`

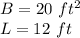
substitute

`V=20(12)=240\ ft^(3)`

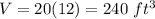
Part c)

step 1

Calculate the area of the trapezoid for h=2 ft (the half)

the length of the midsegment of the trapezoid is (8+2)/2=5 ft

`A=(1)/(2)(5+2)(2)=7\ ft^(2)`

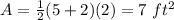
step 2

Find the volume

The volume is equal to

`V=BL`

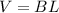
where

B is the area of the trapezoidal face

L is the length of the trough

we have

`B=7\ ft^(2)\\ L=12\ ft`

substitute

`V=7(12)=84\ ft^(3)`