Answer:
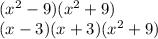
Explanation:
To factor the expression, factor as a difference of squares. Find the square root of each term and write it in this form (x+a)(x-a).
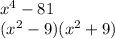
Factor x² - 9 as a difference of squares.
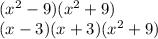
This is the most factored form because a sum of squares cannot be factored.