Question

Part A: Explain why the x-coordinates of the points where the graphs of the equations y = 2x and y = 4x−2 intersect are the solutions of the equation 2x = 4x−2. (4 points)

Part B: Make tables to find the solution to 2x = 4x−2. Take the integer values of x between −4 and 4. (4 points)

Part C: How can you solve the equation 2x = 4x−2 graphically? (2 points)

Answer 1

When X= 1 both graphs are in (1,2)

Explanation:

In order to evaluate the first part, where the lines intersect is you just have to equalize in opposite sides of the equation both equations:

2x=4x-2

Then you have to clear the x

2x-4x=-2

-2x=-2

x=
`(-2)/(-2)`

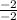
x=1

So your coordinates are x=1, and the Y coordinate you just evaluate one of the equations:

y=4x-2

y=4(1)-2

y=4-2

y=2

So your coordinate for y=2.

Part B, table.

To evaluate this, you just make a table, giving values to x, and you evaluate the Y:

X----Y

-4 -8

-3 -6

-2 -4

-1 -2

0 0

1 1

2 4

3 6

4 8

Part C.

YOu just hava to put it into the graph by evaluating with the tables above.

Answer 2

See below.

Explanation:

Part A: You can solve the equations for an x value which make both true. You do this by setting each equation equal and using inverse operations.

2x = 4x - 2

2x - 4x = 4x - 4x - 2

-2x = -2

x = 1

Part B: You can make a table by substituting the values -4 to 4 in each equation and simplifying.

x y = 2x y = 4x - 2

-4 -8 -18

-3 -6 -14

-2 -4 -10

-1 -2 -6

0 0 -2

1 2 2

2 4 6

3 6 10

4 8 14

Part C: You can graph each equation and where they intersect will be the solution. They intersect at (1, 2). This is where they have the exact same x and y value in the table as well.