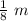Answer:
The length of each side of the cube is
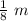
Explanation:
we know that
The volume of a cube is equal to
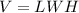
but remember that in a cube
Length, width and height have the same value
so
Let
b-----> the length side of the cube
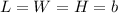
substitute in the formula
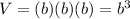
In this problem we have
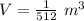
substitute and solve for b
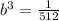
![b=\sqrt[3]{(1)/(512)}\\ \\b=(1)/(8)\ m](https://img.qammunity.org/2020/formulas/mathematics/middle-school/xgcw0viohjn67dbi6rwcbi4t3b8vh5sy6l.png)
therefore
The length of each side of the cube is