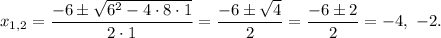Answer:
The next step is to put all terms into the left side of the equation and group the like trems
Explanation:
The first step in determining the solution to the system of equations,
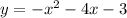 and
and
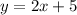 , algebraically is to set the two equations equal as
, algebraically is to set the two equations equal as
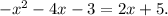
The next step is to put all terms into the left side of the equation and group the like trems:
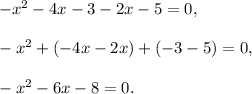
Now you can multiply this equation by -1:
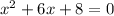
and solve it using quadratic formula: