Question

What value of k causes the terms 7, 6k, 22 to form an arithmetic sequence?

29/12

5/4

11/6

5/2

Answer 1

`k=(29)/(12)`

Explanation:

The given sequence is 7, 6k, 22.

For this to be an arithmetic sequence, there must be a common difference.

`6k-7=22-6k`

Group similar terms;

`6k+6k=22+7`

Simplify;

`12k=29`

Divide by 12

`k=(29)/(12)`

Answer 2

Answer: first option

Explanation:

To form an arithmetic sequence, you have that for the sequence
`7,6k,22`:

`6k-7=22-6k`

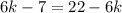
Therefore, to calculate the value of k to form an arithmetic sequence, you must solve for k, as following:

- Add like terms:

`6k+6k=22+7\\12k=29`

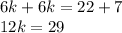
- Divide both sides by 12. Then you obtain;

`k=(29)/(12)`