Calculate the volume of the cone
To start calculating the volume of the cone, we obtain the following data:
To calculate the volume of a cone, we apply the following formula:
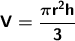 , where
, where
- V = volume
- h = height
- r = radius
- π = pi
We solve, substituting our data in the formula:
taking the square root
Multiplying
Dividing
Therefore the volume of the cone is 144 cm³.