The first shape is a right triangle composed with a semi circle.
The right triangle has a height of 50cm, and its base is the diameter of the circle, which is twice the radius, which is 30cm.
So, the area of the triangle is
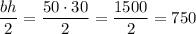
The area of the circle is simply

So, the area of the shape is
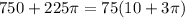
The second shape is the difference between an outer circle and an inner one. The area is thus the difference of the two areas: let
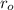 be the outer radius and
be the outer radius and
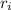 be the inner one. The area of the shape is
be the inner one. The area of the shape is
