Question

Solve by using proper methods.

Let's say that we had a 750 coyotes that were decreasing at a rate of 3% per year. How many years would it be until we had only 100 coyotes left? Show your work.

Answer 1

Approximately after 66.15 years, there will be 100 coyotes left

Explanation:

We can use the formula
`F=P(1+r)^t` to solve this.

Where

F is the future amount (F=100 coyotes)

P is the initial amount (P=750 coyotes)

r is the rate of decrease per year (which is -3% per year or -0.03)

t is the time in years (which we need to find)

Putting all the information into the formula we solve.

Note: The logarithm formula we will use over here is
`ln(a^b)=bln(a)`

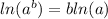
So, we have:

`F=P(1+r)^t\\100=750(1-0.03)^t\\100=750(0.97)^t\\(100)/(750)=0.97^t\\(2)/(15)=0.97^t\\ln((2)/(15))=ln(0.97^t)\\ln((2)/(15))=tln(0.97)\\t=(ln((2)/(15)))/(ln(0.97))\\t=66.15`

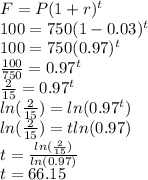
Hence, after approximately 66.15 years, there will be 100 coyotes left.

Rounding, we will have 66 years