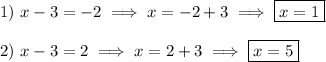Question

Solve algebraically:

Answer 1

`\huge\text{Hey there!}`

`\huge\textbf{Equation a.}`

`\rm{2x^2 - 162 = 0}`

`\huge\textbf{Solving for:}`

`\rm{2x^2 - 162 = 0}`

`\huge\textbf{Add \boxed{\bf 162} to both sides:}`

`\rm{2x^2 - 162 + 162 = 0 + 162}`

`\huge\textbf{Simplify it:}`

`\rm{2x^2 = 0 + 162}`

`\rm{2x^2 = 162}`

`\huge\textbf{Divide \boxed{\bf 2} to both sides:}`

`\rm{(2x^2)/(2) = (162)/(2)}`

`\huge\textbf{Simplify it:}`

`\rm{x^2 = (182)/(2)}`

`\rm{x^2 = 81}`

`\huge\textbf{Take the square root of \boxed{\bf 81}}`

`\rm{x = \pm √(81)}`

`\rm{x = 9\ or\ x = -9}`

`\huge\textbf{Therefore, your answer should be:}`

`\huge\boxed{\textsf{x = } \frak{9\ or } \ \textsf{x = }\frak{-9}}\huge\checkmark`

`\huge\textbf{Equation b.}`

`\rm{-(1)/(2)(x - 3)^2 = -2}`

`\huge\textbf{Solving for:}`

`\rm{-(1)/(2)(x - 3)^2 = -2}`

`\huge\textbf{Simplify both sides of your equation:}`

`\rm{-(1)/(2)x^2 + 3x - (9)/(2) = -2}`

`\huge\textbf{Subtract \boxed{\bf -2} to both sides:}`

`\rm{-(1)/(2)x^2 + 3x - (9)/(2) - (-2) = -2 - (-2)}`

`\huge\textbf{Simplify it:}`

`\rm{- (1)/(2)x^2 + 3x - (5)/(2) = 0}`

`\huge\textbf{Now, we can convert the equation to:}`

`\rm{-0.5x^2 + 3x - 2.5 = 0}`

`\large\text{When we changed the equation entirely, we made it easier to solve}\uparrow`

`\huge\textbf{Use the quadratic formula to solve.}`

`\large\textsf{The quadratic formula:}`

`\mathsf{x= (-b \pm √(b^2 - 4ac))/(2a)}`

`\huge\textbf{Here are your labels:}`

`\text{a = }\rm{-0.5}\\\\\text{b = }\rm{ 3}\\\\\rm{c = }\rm{\ -2.5}`

`\huge\textbf{Your new equation:}`

`\rm{x = (-(3) \pm √(3^2 - 4(-0.5)(-2.5)))/(2(-0.5))}`

`\huge\textbf{Simplify it:}`

`\rm{x = (-3 \pm √(4))/(-1)}`

`\rm{x = 1\ or \ x = 5}`

`\huge\textbf{Therefore, your answer should be: }`

`\huge\boxed{\textsf{x = }\frak{1}\ \textsf{or x = }\frak{5}}\huge\checkmark`

~

Answer 2

`a)\ x_1=-9,\ x_2=9\\\\b)\ x_1=1,\ x_2=5`

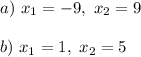
Explanation:

Given equations:

`a)\ 2x^2 - 162 = 0\\\\b) -(1)/(2)(x-3)^2=-2`

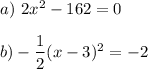
A) 2x² - 162 = 0

Step 1: Divide both sides by 2.

`\\\implies (2x^2 - 162)/(2) = (0)/(2)\\\\\implies x^2-81=0\\\\\implies x^2=81`

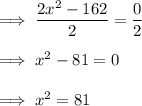
Step 2: Take the square root of both sides (using both the positive and negative roots).

`\\\implies √(x^2)=√(81)\\\\\implies x=\pm\ 9`

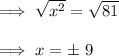
Step 3: Separate into two cases.

`\implies x_1 = -9,\ x_2 =-9`

----------------------------------------------------------------------------------------------------------------

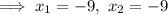
B) -1/2(x - 3)² = -2

Step 1: Multiply both sides by -2.

`\\\implies -2\left(-(1)/(2)(x-3)^2\right)=-2(-2)\\\\\implies (x-3)^2=4`

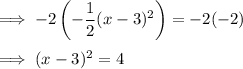
Step 2: Take the square root of both sides (using both the positive and negative roots).

`\\\implies√((x-3)^2)=√(4)\\\\\implies x-3=\pm\ 2`

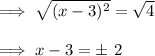
Step 3: Separate into two cases and solve each one.
`1)\ x-3=-2\implies x=-2+3\implies \boxed{x=1}\\\\2)\ x-3=2\implies x=2+3\implies \boxed{x=5}`