Question

(___)^2=(secx-1)(secx+1)
Answer:____

Answer 1

tan

Explanation:

(secx - 1)(secx + 1)

Remove parentheses = sec²x - 1

Use the identity: tan²x + 1 = sec²x = tan²x + 1 - 1

= tan²x

tan²x = (secx - 1)(secx + 1)

Answer 2

Answer: The required answer is tan x.

Step-by-step explanation: We are given to complete the following trigonometric identity :

`(\_\_\_\_\_)^2=(\sec x-1)(\sec x+1).`

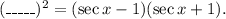
We will be using the following identity from trigonometry to complete the given identity :

`1+\tan^2\theta=\sec^2\theta\\\\\Rightarrow \sec^2\theta-1=\tan^2\theta~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

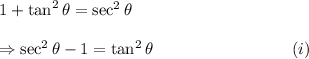
Now, we have

`(\sec x-1)(\sec x+1)\\\\=\sec^2x-1\\\\=\tan^2x~~~~~~~~~~[\textup{from equation (i)}]\\\\=(\tan x)^2.`

Thus, the complete identity is

`(\tan x)^2=(\sec x-1)(\sec x+1).`

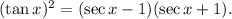
Thus, the required answer is tan x.