Answer:
98 pounds
Explanation:
Let A be pounds of A-type coffee and B be pounds of B-type coffee.
We can set-up two equations and solve simultaneously.
"This month, Hong made 170 pounds of the blend":

"Type A coffee costs Hong $5.75 per pound, and type B coffee costs $4.10 per pound ... a total cost of $858.70":

Now we can multiply first equation by -5.75 and then ADD UP this new equation and equation 2 to get B. We have:
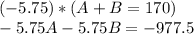
Now solving for B:
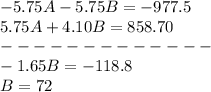
B = 72
Now plugging in this value into B of original first equation and solving for A gives us:
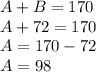
Thus, he used 98 pounds of Coffee A.