Answer:
C
Explanation:
We can use 3 properties here to write this as single logarithm:
1. Log (a^b) = b Log a
2. Log x + Log y = Log (x*y)
3. Log x - Log y = Log (x/y)
We can use property #1 first to write:
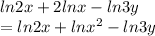
Now we can use property #2 and property #3 to write this as single logarithm:
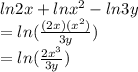
Answer choice C is right.