Answer:
Option C is correct.
Explanation:
Felipe transferred a balance of $3700 to a new credit.
The card had an introductory offer of 5.9% APR for the first 4 months and after that 17.2 % APR.
The card compounds interest monthly, that gives n = 12
So, the equation that represents Felipe's balance at the end of the year will be:
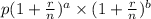
Here a is the introductory rate number of months that is 4
And b is the rest of the standard months that is 8
So, the expression becomes:
