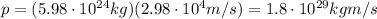Question

Calculate the magnitude of the linear momentum for the following cases.(a) a proton with mass 1.67 Calculate the magnitude of the linear momentum for 10-27 kg, moving with a speed of 5.45 Calculate the magnitude of the linear momentum for 106 m/skg ? m/s(b) a 16.0-g bullet moving with a speed of 435 m/skg ? m/s(c) a 72.5-kg sprinter running with a speed of 11.0 m/skg ? m/s(d) the Earth (mass = 5.98 Calculate the magnitude of the linear momentum for 1024 kg) moving with an orbital speed equal to 2.98 Calculate the magnitude of the linear momentum for 104 m/s.kg ? m/s

Answer 1

(a)
`9.1 \cdot 10^(-21) kg m/s`

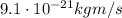
The magnitude of the linear momentum of an object is given by

`p=mv`

where

m is the object's mass

v is its speed

In this case, we have

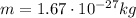`m=1.67\cdot 10^(-27) kg` (mass of the proton)

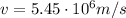`v=5.45\cdot 10^6 m/s` (speed of the proton)

So, the momentum is

`p=(1.67\cdot 10^(-27) kg)(5.45\cdot 10^6 m/s)=9.1 \cdot 10^(-21) kg m/s`

b) 7.0 kg m/s

In this case, we have

m = 16.0 g = 0.016 kg (mass of the bullet)

v = 435 m/s (speed of the bullet)

By applying the same formula, the linear momentum is

`p=(0.016 kg)(435 m/s)=7.0 kg m/s`

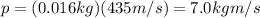
c) 797.5 kg m/s

In this case, we have

m = 72.5 kg (mass of the sprinter)

v = 11.0 m/s (speed of the sprinter)

By applying the same formula, the linear momentum is

`p=(72.5 kg)(11.0 m/s)=797.5 kg m/s`

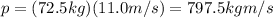
d)
`1.8\cdot 10^(29) kg m/s`

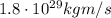
In this case, we have

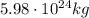`5.98\cdot 10^(24) kg` (mass of the Earth)

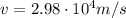`v=2.98\cdot 10^4 m/s` (speed of the Earth)

By applying the same formula, the linear momentum is

`p=(5.98\cdot 10^(24) kg)(2.98\cdot 10^4 m/s)=1.8\cdot 10^(29) kg m/s`