Answer:
The length of the hypotenuse is 26 cm.
Explanation:
In order to find the hypotenuse in this right triangle you can use the Pythagoras' Theorem.
The Pythagorean Theorem tells us that the relationship in every right triangle is:
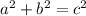 ,
,
See the picture attached to know what is the meaning of constants a, b and c.
In the triangle given, a = 24cm and b = 10 cm, now you can use the Pythagorean Theorem to find c or the hypotenuse.
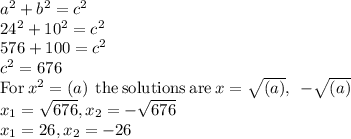
Because we are finding the distance between points AB, this distance cannot be negative, so the answer is the length of the hypotenuse is 26 cm.