You need these two basic solutions and facts to find the equation of a line:
- If you know the gradient
 and one point
and one point
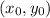 :
:

- If you know the gradient two points
 :
:
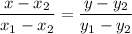
- The slope of a line is the coefficient m when you write it in the
 form
form - Parallel lines have the same slope
- The slopes of perpendicular lines give -1 when multiplied
We can use this list to solve all the exercises:
b)
Use the first equation to get

c)
Use the second equation to get
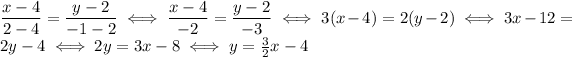
d) same as c)
e) We derive the slope of the line by writing it as

So, the slope is -1/5. From here, it's the same as b)
f) same as e)
g) Again we find the slope as
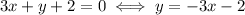
so the slope is -3, and a perpendicular line has slope 1/3. From there, it's the same as b).