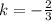Answer:
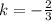
Explanation:
By definition, a direct varition is expressed as following:
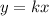
Then, y is directly proportional to x and k is the constant of variation.
Therefore, given the direct variation:
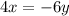
You must solve for the variable y as you can see below:
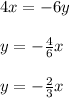
Therefore, as you can see, the constant of variation is the following: