Answer:
Option B - The parabola is narrower.
Explanation:
Given : The function
 is transformed to
is transformed to
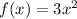
To find : Which statement describes the effect(s) of the transformation on the graph of the original function?
Solution :
When the function of parabola
 is transformed by 'a' unit
is transformed by 'a' unit
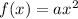
Then,
 makes the parabola narrow.
makes the parabola narrow.
and
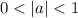 makes the parabola wide.
makes the parabola wide.
On comparing with given function,
|a|=|3| >1 which is greater than 1.
Which means it makes the parabola narrow.
Therefore, the parabola is narrower.
So, Option B is correct.