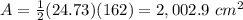Answer:
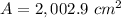
Explanation:
we know that
The area of a regular polygon is equal to
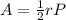
where
r is the apothem
P is the perimeter
step 1
Find the perimeter
The perimeter of a regular nonagon is

where
n is the number of sides (n=9)
s is the length side (s=18 cm)
substitute
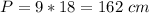
step 2
Find the apothem
The apothem in a regular polygon is equal to
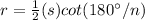
we have
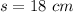
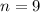
substitute
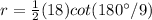
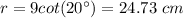
step 3
Find the area of the regular nonagon
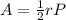
substitute