Answer:
All sides of the triangle are a = 34, b = 27 and c = 46.7
and angles are A = 46°, B = 34.83° and C = 99.17°
Explanation:
In a given triangle A = 46°, a = 34 units and b = 27 units
Then we have to find all angles and measure of the side left.
By sine rule,

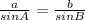

sinB =

sinB = 0.5712
B =
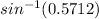
B = 34.83°
Since in a triangle,
∠A + ∠B + ∠C = 180°
46°+ 34.83° + ∠C = 180°
80.83° + ∠C = 180°
∠C = 180 - 80.83 = 99.17°
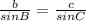
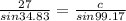
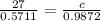
c =
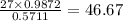
Therefore, all sides of the triangle are a = 34, b = 27 and c = 46.7
and angles are A = 46°, B = 34.83° and C = 99.17°