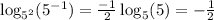Question

Evaluate each log without a calculator


`log_(243^(27) )`


`log_(25) (1)/(5)`

Answer 1

QUESTION 1

The given logarithm is

`\log_(243)(27)`

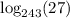
Let
`\log_(243)(27)=x`.

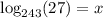We rewrite in exponential form to get;

`27=243^x`

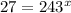
We rewrite both sides of the equation as an index number to base 3.

`3^3=3^(5x)`

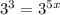
Since the bases are the same, we equate the exponents.

`3=5x`

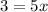
Divide both sides by 5.

`x=(3)/(5)`

`\therefore \log_(243)(27)=(3)/(5)`

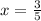
QUESTION 2

The given logarithm is

`\log_(25)((1)/(5) )`

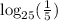
We rewrite both the base and the number as power to base 5.

`\log_(5^2)(5^(-1))`

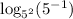
Recall that:
`\log_(a^q)(a^p)=(p)/(q) \log_a(a)=(p)/(q)`

We apply this property to obtain;

`\log_(5^2)(5^(-1))=(-1)/(2)\log_5(5)=-(1)/(2)`