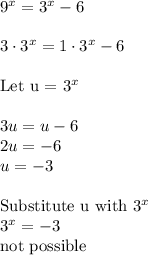Answer: x = 2
Explanation:
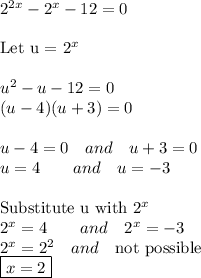
********************************************************************************
Answer: x = 0
Explanation:
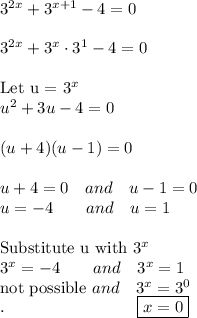
********************************************************************************
Answer: No Solution
Explanation:
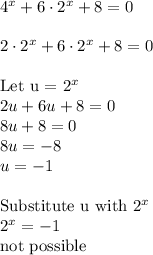
********************************************************************************
Answer: No Solution
Explanation: